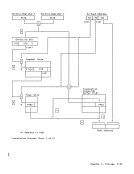
2. +57 = 0011 1001 -35 = 1101 1101 +22 = 0001 0110 No overflow --carry
into leftmost posi
tion and carry out
3. +35 =0010 0011 -57 = 1100 0111 -22 = 1110 1010 Sign change only -
no carry into left
most position and no
carry out
4. -57 =1100 0111 -35 = 1101 1101 -92 = 1010 0100 No overflow --carry
into leftmost posi
tion and carry out
5. +57 =0011 1001 +92 = 0101 1100 +149 =*1001 0101 *Overflow -- carry
into leftmost posi
tion, no carry out
6. -57 =1100 0111 -92 = 1010 0100 -149 =*0110 1011 *Overflow -- no carry
into leftmost posi
tion but carry out
The presence or absence of an overflow
condition may be recognized from the
carries:
2 31 _1
= 2 147 483 647 =0 111 1111
2
16
= 65 536 =0 000 0000 2° = 1 = 0 000 0000 0 = a = a 000 0000 -2° = -1 = 1 111 1111
-2
1
= -2 = 1 111 1111
-2
16
= -65 536 = 1 111 1111
-2
31
+1 = -2 147 483 647 = 1000 0000 -2
31
= -2 147 483 648 = 1000 0000 32-Bit Signed Binary Integers
11110000 0000 0000 1111
1111
11110000 0000 • There is no overflow:
a. If there is no carry into the
leftmost bit position and no
carry out (examples 1 and 3).
b. If there is a carry into the
leftmost position and also a
carry out (examples 2 and 4).• There is an overflow:
a. If there isa carry into the
leftmost position but no carry
out (example 5).
b. If there is no carry into the
leftmost position but there is
a carry out (example 6).
The following are 16-bit signed binary
integers. The first is the maX1mum
positive 16-bit binary integer. The
last1S the maximum negative 16-bit
binary integer (the negative 16-bit
binary integer with the greatest abso
lute value).
2
15
_1 = 32,7672° a -2° -2
15
1a -1
= -32,768
=
=
=
=0 111 1111 1111 1111
=0 000 0000 0000 0001 = 0 000 0000 0000 0000 = 1 111 1111 1111 1111
= 1000 0000 0000 0000 The following figure illustrates several
32-bit signed binary integers arranged
in descending order. The first is the
maximum positive binary integer that can
be represented by 32 bits, and the last
is the maximum negative binary integer
that can be represented by 32 bits.
1111 1111 1111 1111 11110001 0000 0000 0000 0000 0000 0000 0000 0000 0001 0000 0000 0000 0000 0000 1111 1111 1111 1111 1111
1111 1111 1111 11111110 1111 0000 0000 0000 0000 0000 0000 0000 0000 0001 0000 0000 0000 0000 0000 Appendix A. Number Representation and Instruction-Use Examples A-3
into leftmost posi
tion and carry out
3. +35 =
no carry into left
most position and no
carry out
4. -57 =
into leftmost posi
tion and carry out
5. +57 =
into leftmost posi
tion, no carry out
6. -57 =
into leftmost posi
tion but carry out
The presence or absence of an overflow
condition may be recognized from the
carries:
2 31 _1
= 2 147 483 647 =
2
16
= 65 536 =
-2
1
= -2 = 1 111 1111
-2
16
= -65 536 = 1 111 1111
-2
31
+1 = -2 147 483 647 = 1
31
= -2 147 483 648 = 1
1111
1111
1111
a. If there is no carry into the
leftmost bit position and no
carry out (examples 1 and 3).
b. If there is a carry into the
leftmost position and also a
carry out (examples 2 and 4).
a. If there is
leftmost position but no carry
out (example 5).
b. If there is no carry into the
leftmost position but there is
a carry out (example 6).
The following are 16-bit signed binary
integers. The first is the maX1mum
positive 16-bit binary integer. The
last
binary integer (the negative 16-bit
binary integer with the greatest abso
lute value).
2
15
_1 = 32,767
15
1
= -32,768
=
=
=
=
=
= 1
32-bit signed binary integers arranged
in descending order. The first is the
maximum positive binary integer that can
be represented by 32 bits, and the last
is the maximum negative binary integer
that can be represented by 32 bits.
1111 1111 1111 1111 1111
1111 1111 1111 1111