Decimal integers consist of
decimal digits and a sign. Each digit
and the sign are represented by a 4-bit
code. The decimal digits are in
binary-coded decimal
the values
minus. These are the preferred sign
codes, which are generated by the
machine for the results of decimal
arithmetic operations. There are also
several alternate sign codes
minus). The alternate sign codes are
accepted by the machine as valid
for results.
Decimal integers may have different
are two decimal formats: packed and
zoned. In the packed format, each byte
contains two decimal digits, except for
the rightmost byte, which contains the
sign code in the right half. For deci
mal arithmetic, the number of decimal
from one to 31. Because decimal inte
gers must consist of whole bytes and
there must be
the number of decimal digits is always
odd. If an even number of significant
digits is
be inserted on the left.
In the zoned format, each byte consists
of a decimal digit on the right and the
zone code 1111 (F hex) on the left,
except for the rightmost byte where the
sign code replaces the zone code. Thus,
a decimal integer in the zoned format
can have from one to 16 digits. The
zoned format may be used directly for
input and output in the extended
binary-coded-decimal interchange code
separated from the rightmost digit and
handled as
positive (unsigned) numbers, however,
the sign can simply be represented by
the zone code of the rightmost digit
because the zone code is one of the
acceptable alternate codes for plus.
In either format, negative decimal inte
gers are represented in true notation
with a separate sign. As for binary
integers, the radix point (decimal
point) of decimal integers
to be fixed at the right, and any scal
ing
The following are some examples of deci
mal integers shown in hexadecimal nota
tion:
+123 12
12 3F F1 F2 F3
-4321
minus sign (negative zero) is produced.
For example, the multiplicand:
times the multiplier:
algebraic rule of signs even when the
value is zero. A negative zero,
however, is equivalent to a positive
zero in that they compare equal in a
decimal comparison.
FLOATING-POINT NUMBERS
A floating-point number is expressed as
a hexadecimal fraction multiplied by a
separate power of 16. The term floating
point indicates that the placement, of
the radix (hexadecimal) point, or scal
ing, is automatically maintained by the
machine.
The part of a floating-point number
which represents the significant digits
of the number is called the fraction. A
second part specifies the power (expo
nent) to which 16 is raised and indi
cates the location of the radix point of
the number. The fraction and exponent
may be represented by 32
format), 64 bits (long format), or 128
bits (extended format).
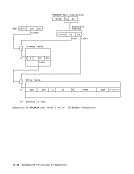
Short Floating-Point Number
IsICharacter;st;cI6-D;9;t
Appendix A. Number Representation and Instruction-Use Examples A-5